简称神经网络(NN),是目前各种神经网络的基础,其构造是仿造生物神经网络,将神经元看成一个逻辑单元,其功能是用于对函数进行估计和近似,是一种自适应系统,通俗的讲就是具备学习能力。
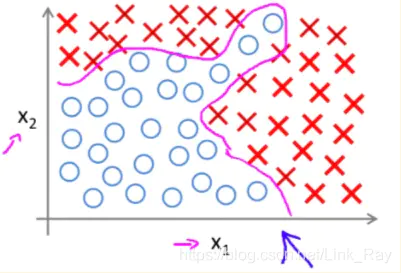
其作用,目前为止就了解到分类。其目的就是在圈和叉之间画出一条分界线,使得接下来我们可以根据其位置来预测其属于哪个分类。这个图只有两种分类,实际上可以有非常多种,但其网络结构也会变得复杂,可以说一层网络可以画一条线,多层网络就可以画多条线。
其内部最主要的构造就是神经元,如下图所示
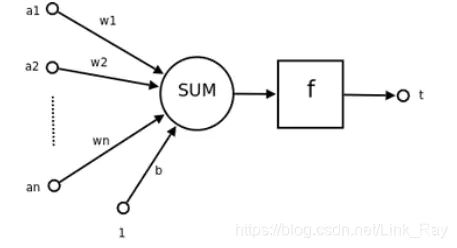
这张图有五个部分组成
输入向量
权重
求和
激励函数
输出
可以把权重,求和,激励函数合并在一起,统称为隐藏层,输入的向量可以成为输入层,输出的向量可以称为输出层。
因此神经网络的基础结构便是三层结构
输入层
隐藏层
输出层
输入层
一般有输入向量有多少维,输入层就会有多少个输入单元,每个单元代表一维向量,相当于该事物的特征,其与隐藏层的结点呈现为全连接状态。即1-N的关系。
隐藏层
隐藏层可以有许多层,层数越多神经网络的处理能力就越强,但相对的性能也会下降,每一层隐藏层可以针对某一种特征进行处理,例如一层隐藏层处理图像的斜线,一层隐藏层处理图像的灰度等等。
连接到隐藏层的每一条边都有一个权重w,这个其实代表的某特征的权重。
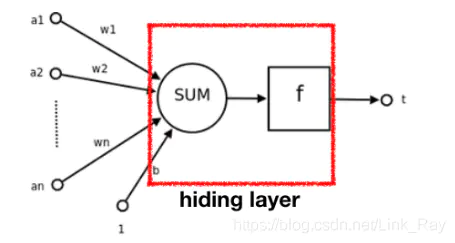
其中f ff是激励函数,1 ∗ b 1*b1∗b为前面层的偏置单元。
其结果A AA就被传递到输出单元。
输出层
结果A AA被传递到输出单元,到这一步为止,可以被称作为前向传播。然后将其结果与训练集中的期望结果进行比对,用损失函数,得出损失值,通俗的讲就是与正确结果的差距,损失函数如下所示

反向传播
其证明原理十分复杂,暂时还未弄懂。简要的过程便是,其会根据训练集( x , y ) (x,y)(x,y)中,x xx在神经网络中跑出来的结果h与y进行比对,然后根据比对结果反向更新每一层的权重w,这里必须是反向一层一层的更新,逐层传递,从而使得J ( θ ) J(\theta)J(θ)变小,即最小化损失函数。
从而便达到了神经网络的学习效果,其能根据训练集来反向更新权重,使得下一次的输出结果h和y之间的差距变小,从而达到更优。
激励函数
激励函数也叫点火规则,这使它与人脑的工作联系起来。当一个神经元的输入足够大时,就会点火,也就是从它的轴突(输出连接)发送电信号。同样,在人工神经网络中,只要输入超过一定标准时才会产生输出,这就是点火规则的思想。当只处理二值输出时,输出要么为0要么为1,取决于神经元是否应该点火。
卷积神经网络(CNN)
目前只了解到卷积神经网络用于图像处理的方面。
其与神经网络(NN)不同之处再于多了几层结构,相当于对输入做了预处理。
卷积神经网络的结构:
输入层
卷积层
池化层
全连接层
输出层
其中全连接层就相当于神经网络当中的隐藏层。对于一张图像来说,在计算机当中其是一个三维结构,有着长,宽,高三个特征,其中长和宽组成一个矩阵,高(channel)代表多个矩阵,例如RGB三种颜色则有三个矩阵,这张图片高度为3.
卷积层
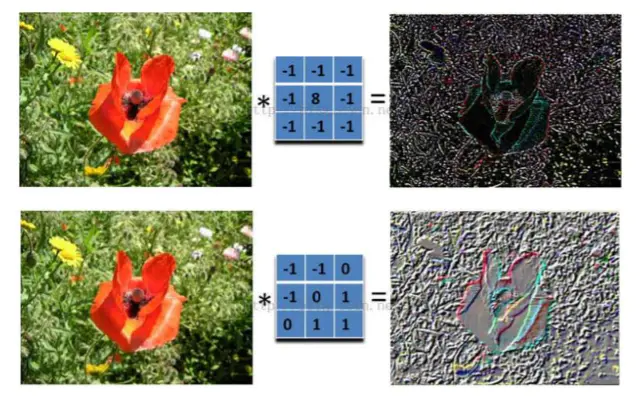
使用多个filter在图像上面做内积,得出多个特征,卷积的过程就是拿一个矩阵在原图矩阵上面边移动,边做内积,最后得出一个比原图小一点的矩阵。如图所示,一个9*9的矩阵被filter后变成了-8。
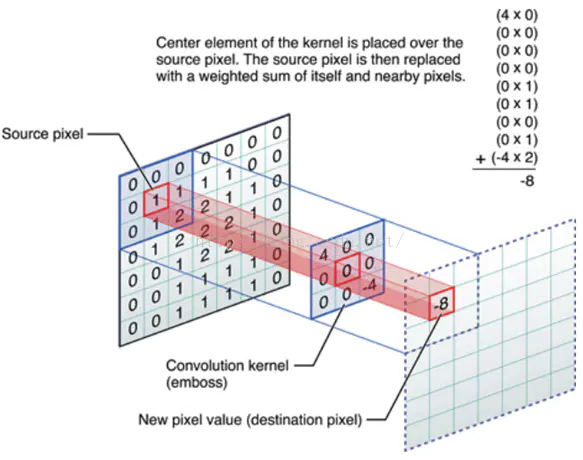
而这个filter的作用其实在视觉上的效果便是提取图片的某些特征,例如颜色的深浅与轮廓。
池化层
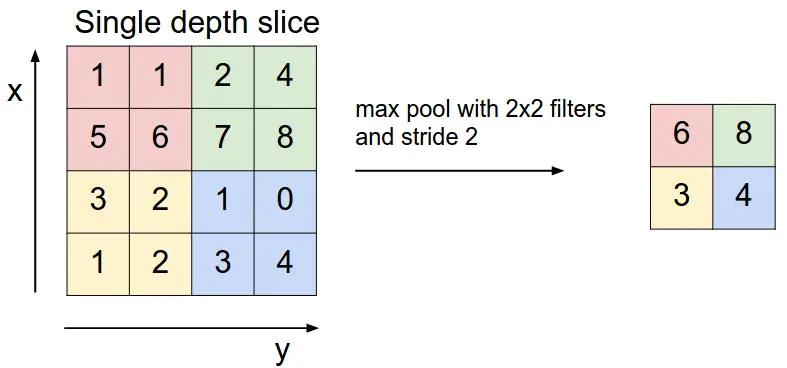
池化层的作用目前还未完全弄明白,似乎好像只是缩小数据,例如对于卷积出来的矩阵,对于每2 * 2个小矩阵,提取其中最大的值代表这个2 * 2矩阵的值,使得原矩阵再次缩小。即取区域平均最大值。
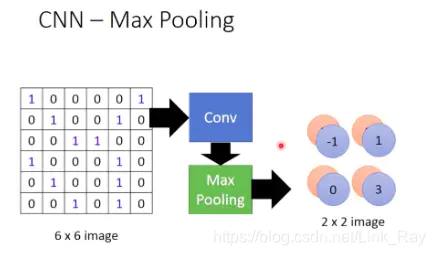
当一个灰度图片矩阵做完卷积和最大池化后,结果如下
为何要用CNN呢?
在图像分类当中,当我们要识别这张图片是不是鸟时,我们会分几个特征来识别,是否有翅膀,是否有喙,是否有尾巴,这些特征一般只是图片的一小部分,如果用NN来做的话,判断每个特征都会输入整张图片,那样利用率太低了而且参数太多,而对于CNN来说,它会通过卷积层,以及池化层来压缩输入数据的大小,即将数据分割成许多分小数据。
即卷积神经网络不在针对于图片上一个点做处理,而是对一块区域做处理。
从而使得神经网络当中的神经元输入数目减少,即用了较少的参数。
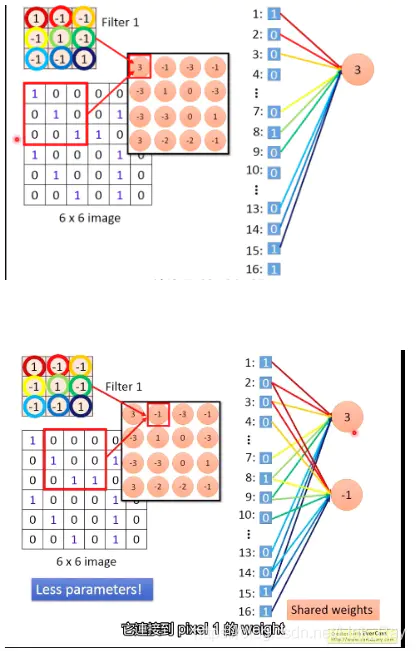
如图所示,原本对于一个神经元,原本要连接36个输入单元,现在只需连接9个输入单元即可。将输入的参入减小,而且还能让两个神经元公用一些weight。
一张1层28x28的图片矩阵经过两次卷积和池化后变成50层5x5的图片矩阵
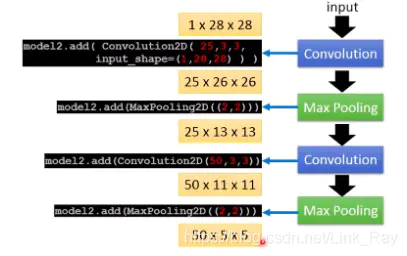
整个卷积神经网络的过程
